ОПРЕДЕЛЕНИЕ ВИДА ОСОБЫХ ТОЧЕК

Как отмечалось, фазовые траектории обладают тем свойством, что они нигде не пересекаются, за исключением «осо­бых» точек или точек «покоя» системы. При этом фазовые траекто­рии могут либо «входить» в особую точку (в этом случае особая точка соответствует состоянию устойчивого равновесия), прохо­дить мимо, либо «выходить» из нее — неустойчивое равновесие. Подробное исследование движения летательного аппарата в фа­зовом пространстве с нахождением фазовых траекторий во всех точках этого пространства весьма сложно и в этом нет необходи­мости. Существенно больший интерес представляет более простая задача — задача нахождения положения особых точек в фазовом

пространстве и исследования движения летательного аппарата в их окрестности.

Задача определения вида особой точки сводится к анализу движения в ее окрестности, т. е. к исследованию движения «в ма­лом» и поэтому вплотную примыкает к проблеме анализа устой­чивости движения вблизи особой точки. При этом знание и исполь­зование критериев устойчивости либо неустойчивости движения позволяет определять, к какому типу относится рассматриваемая особая точка, а главное — может ли практически быть реализовано движение в ее окрестности. Представим, как это обычно делается при линеаризации уравнений, параметры движения самолета в виде

а =; аст -|- Да;

($2 ■ 0-f "I — A (Dr,

Р — Рст -I — Ар; (ЮЛ)

toy СТ А,

(D* — С0д0 ~j — А(0а.

Выполняя обычную процедуру линеаризации уравнений (2.14), получим систему однородных уравнений в вариациях (для’сокра­щения записи знак вариации в уравнениях опущен):

а “ТГ ~2 а ~Ь РР^хО pPct^jc = 0;

(oz — rnzC)a — mjwz — j — ^|.io)Ao(o(/ — j- Л|ко„ стюА = 0; (10.2)

4 _

P‘ — 11»</—- 2“ P — И (фг + «ст)»лг’— !Ші0а = 0;

Щ — ГПуp — Шуу<£>У — B^l(OxCtOz — BlUOz CT(0X = 0;

— / — (0 —- — ——- ——— D / — ————- (j) —

cox — mx (Ox + С[ЛЫУ стсог — mx6 — VCpco* CT — j — mxy) ыу — 0.

Для нахождения условий устойчивости необходимо рассма­тривать характеристическое уравнение системы уравнений (10.2), которое в общем случае может быть записано в виде

К5 + В41* + В3№ + В2Х2 + Вг1 + В0 = 0. (10.3)

Условиями устойчивости решений системы уравнений (10.2) согласно критерию устойчивости Рауса—Гурвица является вы­полнение системы неравенств

В0 > 0; Вх > 0; В2>0; В3> 0; В4>0;

/?, = ВАВ3 — В2 > 0; (Ю.4)

Rt — Вх (В2ВХ — В3В0) — (В4В4 — В0)2 ^ 0.

Условия устойчивости (10.4), записанные в виде зависимостей между аэродинамическими и инерционными характеристиками самолета, сложны и практически могут быть использованы только при проведении расчетов на вычислительных машинах. Исключе­ние составляет критерий апериодической устойчивости В0 > О, который определяет устойчивость во многих практически важных случаях и может быть получен в достаточно простом виде.

Из системы уравнений (10.2) следует, что выражение для В0 можно получить, если раскрыть определитель

Во = са У 2 —И рсі)*0 0 llf^CT 1 31 — О) mzi 0 3 1 О ст ср [1 (срг С*ст) —Нсо*о 0 Z 2 —ц 0 —Диыхо —ml —туу ./ЗрСО^ ст 0 С* |ясо у ^ —ml — (CflW2CT — fm/) —<*х —тх

(10.5)

В определителе (10.5) пунктиром выделен минор, с помощью которого вычислялся свободный член характеристического урав­нения А0 при анализе движения самолета при установившемся

вращении по крену с со* = const (см. § 5).

Для раскрытия определителя воспользуемся следующим прие­мом. Умножим столбцы с первого по четвертый соответственно на:

d<xст. d, coz ст. *Фст. d(Dy ст с/со* с/со* с/со* скох

и прибавим их к пятому столбцу. Тогда нетрудно убедиться, что в верхних четырех строчках пятого столбца получим производные

по со* от левых частей алгебраических уравнений (10.2), из ко­торых находились статические решения. Поскольку в правых частях этих уравнений стояли постоянные величины, то соответ­ствующие производные по со* как левых, так и правых частей этих уравнений равны нулю. Непосредственной проверкой легко убедиться, что в пятой строке пятого столбца после операции суммирования, получим выражение, равное производной

dAm*CT/dcot. Таким образом, получим, что свободный член ха­рактеристического уравнения системы уравнений (10.2)— опре-

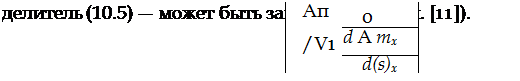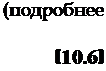Раскрывая определитель (10.6) по элементам последнего столбца, получим окончательное выражение для свободного члена ха­рактеристического уравнения В0 в виде

В0 — А0 d~!flx. (10.7)

dox

На основании соотношения (10.7) необходимое условие устой­чивости В0 > 0 может быть записано в следующем удобном для применения виде. Движение устойчиво, если выполняются не­равенства

^-^>0 при Д>0; (10.8)

«СОх

dAmx <Q при Ло<0 (Ш.9)

dcox

Легко показать, что неравенства (10.8) и (10.9) представляют собой обобщение полученного в гл. 2 условия апериодической устойчивости движения самолета при установившемся вращении относительно продольной оси.

Неравенство В0 > 0 или эквивалентные ему условия (10.8) и (10.9) являются необходимыми, но не достаточными критериями устойчивости. Из неравенства В0 > 0 следует только то, что в ха­рактеристическом уравнении не имеется нечетного количества действительных положительных корней, однако не исключается возможность наличия четного числа положительных действитель­ных корней или любого числа комплексно-сопряженных корней с положительной действительной частью. Обычно характеристиче­ское уравнение (10.3) имеет не более одного положительного корня, в связи с чем критерий устойчивости (10.8) и (10.9) позво­ляет определить апериодическую устойчивость движения самолета в окрестности особой точки, т. е. выделить седловые особые точки. Остальные критерии устойчивости (10.4) упростить не удается.

Остановимся кратко на^некоторых свойствах коэффициентов и корней характеристического уравнения (10.3). Рассмотрим изменения свободного члена характеристического уравнения в окрестности критических угловых скоростей крена. При анализе

движения самолета с сох = const было получено, что свободный член А0 характеристического уравнения обращается в нуль, а затем изменяет знак при переходе через критические угловые

91

скорости крена. В общем случае, когда т* Ф 0, изменения В0 в окрестности критических скоростей могут быть исследованы

следующим образом. Легко показать, что функция Атх (со*) может быть представлена в виде

(шло)

Ар (СОх)

где функция G (со*) не имеет нулей, совпадающих с нулями функции А0 (со*).

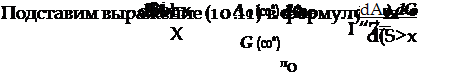Дифференцируя функцию А га* по cov, получим

При переходе через критические скорости крена величина А0

обращается в нуль, а призводная dA0/d(ox не равна нулю. Отсюда следует, что при критических угловых скоростях крена функ­ция В0 (со*) имеет полюс первого порядка, т. е. при приближе­нии параметра со* к критическим значениям (соа, сор) корни характеристического уравнения начинают неограниченно воз­растать.

Легко убедиться, что коэффициент Л4 характеристического уравнения (10.3) не зависит от величины угловой скорости крена оэ*. С другой стороны, известно, что сумма действительных частей всех корней равна этому коэффициенту с обратным знаком, т. е.

Ві = — 23 (2£г + Яг). (10.13)

Таким образом, из соотношения (10.13) следует, что если действительная часть хотя бы одного корня характеристического уравнения начинает возрастать, в частности стремиться к беско­нечно большой величине, то всегда имеется корень, действитель­ная часть которого стремится к бесконечно большим значениям противоположного знака.

Выведенный критерий апериодической устойчивости позволяет определять условия, при которых нарушаются характеристики устойчивости и управляемости самолета. В этой связи несомнен­ный интерес представляет определение зависимости границы

апериодической устойчивости от параметров управления самоле­том (6Э, ф, 6ц).

Рассмотрим возможный вид такой зависимости для частного случая аэродинамических характеристик самолета, когда =

о — —.

= 0 и т’х = const и можно пренебречь произведением CcO^COz в уравнении для со*. Из соотношения для В0 (10.5) видно, что

параметры установившегося движения аст, coZCT, рст, со^ст входят только в последний столбец определителя. Отсюда следует, что свободный член характеристического уравнения В0 является линейной функцией этих параметров.

Используя выражения, следующие из уравнения равновесия сил, можно определить зависимости (0гст и d^CT от аст и |3СТ:

— су

С і ~ “оТГ” &ст Рст^л »

Т (10.14)

СТ = 2и~ Рст (аст + Фг)

Таким образом, условия на границе апериодической устойчивости могут быть представлены в общем случае в виде функции трех параметров аСТ1 рст и с5х:

В0 = а (соА) аст + b (со*) Рст + с (со,) = 0, (10.15)

т. е. уравнениями бифуркаций на плоскости параметров аст, рст будут прямые линии. Соотношение (10.15) можно преобразовать к непосредственной зависимости от параметров управления (ф, бн) самолета. Воспользовавшись выражениями для нахождения ста­тических решений можно записать:

(10.16)

Подставив (10.16) в (10.15), получим вновь линейное уравнение для бифуркационной границы, но теперь в зависимости от пара­метров управления ф, 6Н и величины угловой скорости крена со*:

Во = ai К) ф (со*) 6и -(- с (со*), (10.17)

где аг (со*), Ьх (со*)—функции угловой скорости ооЛ, а

Случай больших угловых скоростей крена

Учитывая, что связь между бэ и в общем случае нелинейная, из соотношения (10.17) можно заключить, что и граница бифур­кационных значений ф, 6Н, 6Э также является нелинейной.

Аналогично можно рассмотреть границу колебательной устой­чивости, подставляя в характеристическое уравнение Д0 (0) = О значение корня равное /со, где со принимает значения от —оо до +оо.

Разделив действительные и мнимые части, получим:

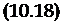Re Д0 (/со, аст, рст, со*) 0;

ІШ До (/(О, CXjyj-, Рст» С0Х) — 0.

Из системы уравнений (10.18), исключив со, можно получить границу области колебательной устойчивости в виде F (аст, Рст» ©х). но эт0 Уже будет некоторая нелинейная функция своих аргументов. В связи с этим такая граница может быть практически рассчитана только на ЦВМ.